ベクトルの基礎を少し学んで、反射ベクトルの求め方がある程度わかった気がしますので、学習ノートを書いておきます。
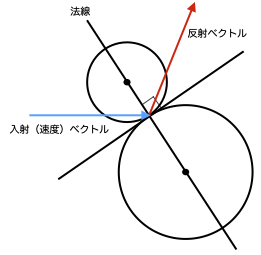
大きい円は静止していて、それに小さい円が青いベクトル方向にぶつかって来たという想定です。
法線ベクトルは、dx = 小さい円のx座標-大きい円のx座標、dy = 小さい円のy座標-大きい円のy座標で、(dx,dy)という要素のベクトルになります。
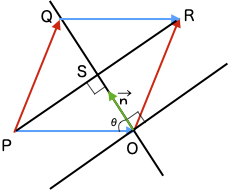
上の図のようにひし形の平行四辺形に対角線を入れた図で考えると、反射ベクトルOR→は、OQ→とQR→の和というベクトルの基礎を学びました。
QR→=PQ→、つまり入射ベクトルと同じ(ベクトルは方向と長さが同じであれば座標位置に関係なく同じ)ですので、OQ→の長さがわかれば(方向は法線ベクトルと同じ)OQ→が求められるので、反射ベクトルOR→も求められるということですよね。

そして、内角θを挟んで入射ベクトルと長さは同じで逆向きのOP→と法線方向の長さ1のベクトルとの内積で算出されるのは辺OSの長さというのがミソのようです。
a→(x1, y1)とb→(x2, y2)の2つのベクトルの内積は、x1*x2+y1*y2ということですし、別の式では、|a→||b→|cosθ と表すとのことです。(|a→|はa→の長さ)
後者の式は、a→先端からb→方向の線上に垂線を下ろした、垂直方向に投影したベクトルの長さ(|a→|cosθ)に|b→|を掛けた数値ということができます。
a→とb→の始点を揃えて、内角をθとすると、cosθ=a→・b→ / |a→||b→| (・は内積計算の意味)らしいので、変形すると、a→・b→ = |a→| |b→| cosθ となります。
ベクトルの基礎で学んだのですが、内積は、2つのベクトルの始点を一致させた場合の内角をθとする計算とのことですので、衝突点を始点とするには、PO→の逆向きのOP→(-PO→)としないと正しい結果はでないのですね。
でも、実は、入射ベクトルの方向のままのPO→とn→を内積計算した結果は符号が逆になるだけで絶対値は同じになるようです。ですので、PO→のまま内積計算をしてその結果に-1を掛ければ結局OKのようですので、そのようにします。
内積計算の式は、法線ベクトルを仮にn→とすると、
PO→・n→ = |PO→| |n→| cosθ
さて、ここで|n→|、つまりn→の長さが1だったらどうでしょうか。OP→とn→の内積は、 |OP→| cosθとなります。辺OPの長さ掛けるcosθですね。これは直角三角形OPSで三角関数から辺OSの長さになります。
n→の長さが1だったらということですので、法線ベクトルを長さが1になるように変換する必要があります。これをnormalizeする、正規化するというそうです。
法線ベクトルの長さをlengthとして、それを1にするということは、lengthを1/lengthにするということですから、法線ベクトル(dx, dy)だとすると、lengthが斜辺で、dxが底辺、dyが高さの直角三角形の関係にありますから、相似的にdxとdyも1/lengthとすることで、斜辺である法線ベクトルは長さが1になります。
上の計算方法で自前の正規化関数を記述できますが、p5.jsには正規化関数が用意されています。
let n = createVector(dx, dy).normalize();
これで法線方向の長さ1のn→が出来上がります。

ということで、速度ベクトル(入射ベクトル)PO→と長さ1にした法線ビクトルn→を内積計算をした結果を符号を逆にすると、OSの長さが求められます。
計算式は、PO→(x1, y1)、長さを1にしたn→(x2, y2)という2つのベクトルの内積=x1*x2+y1*y2 = OSの長さということになります。
内積計算もp5.jsに用意されていて、速度ベクトルvと法線ベクトルnの内積は、
p5.Vector.dot(v, n)
で算出され、この結果の符号を逆にしたものが上の図の辺OSの長さということになります。
OSの長さを2倍にするとOQの長さが出ます。そして、長さ1のn→にOQの長さを掛けるとOQ→というベクトルが得られます。
そうすると、反射ベクトルOR→ = OQ→ + QR→ = OQ→ + 入射ベクトルPO→ということで反射ベクトルを求めることができました。
以上から、反射ベクトルをR→、入射ベクトルをV→、正規化した法線ベクトルをN→とすると、
R = -2 ( V ・ N ) N + V または R = V – 2 ( V・N ) N
と表すことができます。
以上が私の現状の理解です。
実際にp5.jsでコードを書いてみました。こちらのページです。
p5.js 反射ベクトルの勉強
—参考文献—
以下の情報のおかげで大変理解が進みました。
坂田アキラの ベクトルが面白いほどわかる本 (坂田アキラの理系シリーズ)
https://amzn.asia/d/en5Z4ay
C++ 反射ベクトル 「式の解説」Coding Ocean
https://youtu.be/-896y8YXHps?si=TywsoKnc-6IynEGs
